Astronomical Algorithms Implemented

I have been working on several ways to test the accuracy of the model. Beyond noting the sun rise and set times along with local noon on an improvised sun dial (the sunbeam from the skylight on my south facing stairs), I have used a Davis Mark-15 Plastic Sextant with a swimming pool as an artificial horizon. While I have no training other than what came in the instructions with the sextant, on a clam day with a stable reflection I get results within a couple arc minutes of my calculations. I use these results in the source code unit tests.

I also have agreement within a couple minutes of other sites like the NOAA solar calculator and the Astronomical Applications Department of the U.S. Naval Observatory And in references like Wikipedia's midnight sun reference, I get the results they have for the rise, transit and set times for Fairbanks, Alaska, when making the adjustments for time zone they list.

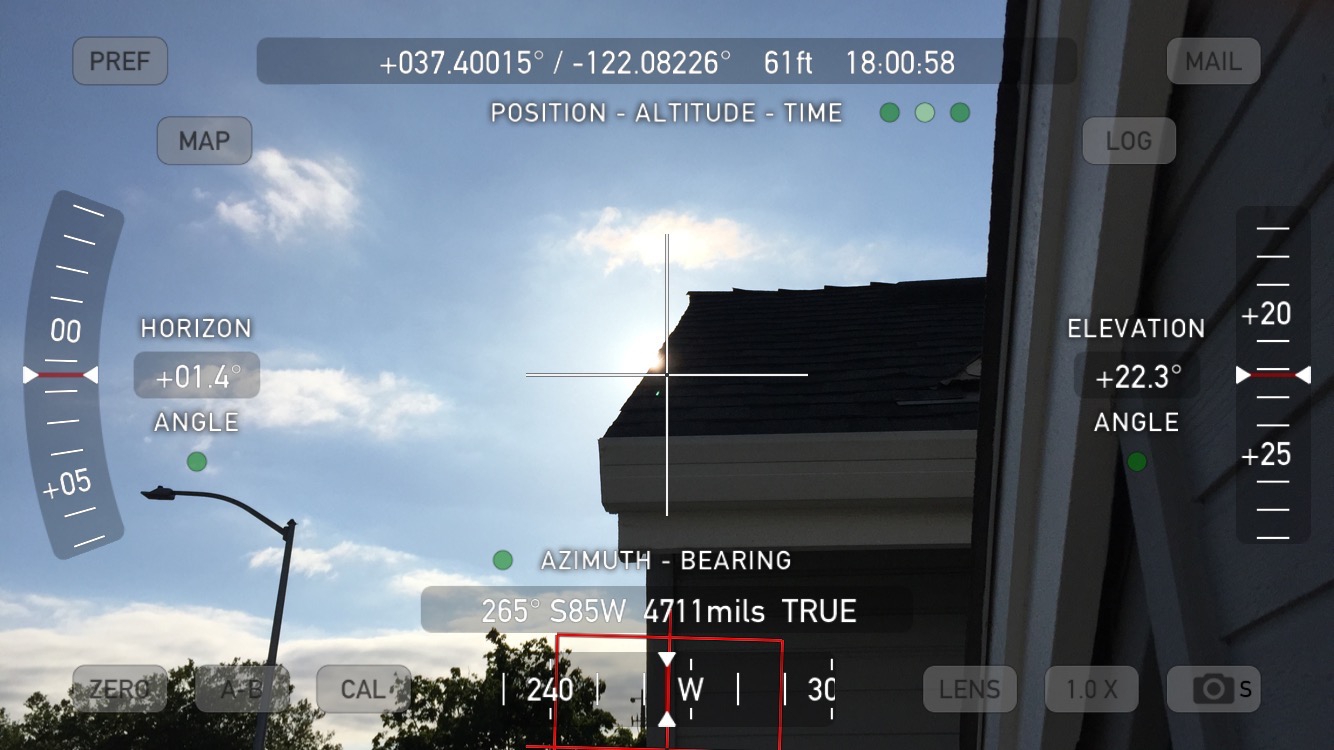
The picture below was taken (on 2016-05-08) with the iOS Theodolite app (I have no connection to them other than as a satisfied customer.) When I enter the time and location coordinates, I get good agreement in altitude (my 22.87° vs. their 22.3°) and am only off by about 10° azimuth (274.73° vs. 265°), and some of that I would attribute to some "stickiness" in the sensors.

From Meeus' Example 13.b, the observer's location is at the U.S. Naval Observatory at Washington, D.C.: Latitude 38:55:17, Longitude -77:03:56 (in my ":" notation for degrees, minutes, seconds and using the IAU positive east convention for latitude instead of Meeus'); Venus' right ascension is 23:09:16.641 hours and declination -6:43:11.61 degrees. On 1987-04-10 at 19:21:00 UT, Venus was 15.215 degrees above the horizon, bearing 248.0335 from the north, which matches Meeus' results after adjusting his bearing of 68.0337 degrees from the south.